What is a backpropagation algorithm?
A backpropagation algorithm, or backward propagation of errors, is an algorithm that's used to help train neural network models. The algorithm adjusts the network's weights to minimize any gaps -- referred to as errors -- between predicted outputs and the actual target output.
Weights are adjustable parameters that determine the strength of the connections between artificial neurons -- also referred to as nodes -- in different layers of a neural network. Specifically, weights determine how much influence the output of one neuron has on the input of the next neuron, which can directly influence the network's output and performance.
Backpropagation is designed to test for errors working back from output nodes to input nodes. It's an important mathematical tool for improving the accuracy of predictions in data mining and machine learning (ML) processes. Essentially, backpropagation is an algorithm used to quickly calculate derivatives in a neural network, which are the changes in output because of tuning and adjustments.
Backpropagation is a fundamental aspect of training deep neural networks, as it enables these networks to learn complex patterns in data by fine-tuning the weights, improving their performance.
What is a backpropagation algorithm in a neural network?
Neural networks are composed of multiple layers of interconnected neurons. These are organized into three main layers: the input layer, the hidden layer and the output layer.
- The input layer receives the raw data features. Each neuron in this layer corresponds to a specific feature in the input data.
- The hidden layer, of which there can be more than one, processes the data it receives. Hidden layer neurons apply weights, biases and activation functions.
- The output layer produces the final output predictions. Neurons in this layer represent different possible outputs of the model.
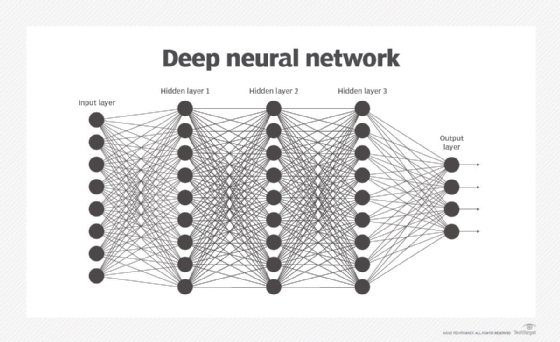
Artificial neural networks (ANNs) and deep neural networks use backpropagation to compute gradients. This is done by passing any error information backward through the network, from the output layer through the hidden layer -- or layers -- to the input layer. The calculated gradients are then used in an optimization algorithm called gradient descent. Gradient descent minimizes errors or gaps between the predicted outputs and the network's actual outputs by adjusting the weights of the network.
In an ML context, gradient descent helps the system minimize the gap between desired outputs and actual system outputs. The algorithm tunes the system by adjusting the weight values for various inputs to narrow the difference between outputs. This is also known as the error between the two.
More specifically, gradient descent provides information on how a network's parameters -- including weights and biases -- need to be adjusted to reduce error. A cost function, which is a mathematical function that measures this error, guides this process. The algorithm's goal is to determine how the parameters must be adjusted to reduce the cost function and improve overall accuracy.
In backpropagation, the error is propagated backward from the output through the hidden layers, enabling the network to calculate how each weight needs to be adjusted. The term backpropagation refers to this process of propagating errors backward, from output nodes to input nodes.
Activation functions can then activate neurons to learn new complex patterns, information and whatever else they need to adjust their weights and biases and mitigate this error to improve the network.
What is the objective of a backpropagation algorithm?
Backpropagation algorithms are used extensively to train feedforward neural networks, such as convolutional neural networks, in areas such as deep learning. A backpropagation algorithm is pragmatic because it computes the gradient needed to adjust a network's weights more efficiently than computing the gradient based on each individual weight. It enables the use of gradient methods, such as gradient descent and stochastic gradient descent, to train multilayer networks and update weights to minimize errors.
Types of backpropagation
The following are two types of backpropagation networks:
- Static backpropagation. This is a network developed to map static inputs for static outputs, meaning that an output can be produced immediately after the input is provided. Static networks can solve static classification problems, such as optical character recognition (OCR).
- Recurrent backpropagation. The recurrent backpropagation network is used for fixed-point learning. This means that during neural network training, the weights are numerical values that determine how much neurons influence perceptrons. They're adjusted so that the network can achieve stability by reaching a fixed value.
The key difference here is that static backpropagation offers instant mapping, while recurrent backpropagation does not.
Advantages and disadvantages of backpropagation algorithms
There are several advantages to using a backpropagation algorithm, but it also comes with challenges.
Advantages of backpropagation algorithms include the following:
- They don't have to tune many parameters aside from the number of inputs.
- They're highly adaptable and efficient, as they don't require domain-specific knowledge to start training.
- They use a standard process that usually works well.
- They're user-friendly, fast and easy to program.
- Users don't need to learn any special functions.
Disadvantages of backpropagation algorithms include the following:
- They prefer a matrix-based approach over a mini-batch approach.
- Data mining is sensitive to noisy data and other irregularities. Unclean data can affect the backpropagation algorithm when training a neural network used for data mining.
- Performance is highly dependent on input data.
- Training is time- and resource-intensive.
While backpropagation has been significant to artificial intelligence (AI) and neural networks, some experts believe its limitations will spur the creation of more advanced learning algorithms in the future.
What is a backpropagation algorithm in machine learning?
Backpropagation is a type of supervised learning since it requires a known, desired output for each input value to calculate the loss function gradient, which is how desired output values differ from actual output. Supervised learning, the most common training approach in machine learning, uses a training data set that has clearly labeled data and specified desired outputs.
The backpropagation training algorithm has emerged as an important part of machine learning applications that involve predictive analytics. In real-world applications, developers and machine learning experts implement backpropagation algorithms for neural networks using programming languages such as Python.
While backpropagation techniques are applied mainly to neural networks, they can't be applied to linear regression, support vector machine and decision tree algorithms -- all of which require different forms of optimization.
What is the time complexity of a backpropagation algorithm?
The time complexity of each iteration -- or how long it takes to execute each statement in an algorithm -- depends on the network's structure. In the early days of deep learning, a multilayer perceptron was a basic form of a neural network consisting of an input layer, hidden units and an output unit. The time complexity was low compared with today's networks, which can have exponentially more parameters. Therefore, the sheer size of a neural network is the primary factor affecting time complexity -- but there are other factors, such as the size of training data sets or the amount of data used to train networks.
Essentially, the number of neurons and parameters directly affects how backpropagation works. During a forward pass, in which input data moves forward from the input layer to the next layer and so on, the time complexity is larger when there are more neurons involved. During the subsequent backward pass, where parameters are adjusted to rectify an error, more parameters also mean more of a time complexity.
What is a backpropagation momentum algorithm?
Using gradient descent optimization algorithms for tuning weights to reduce an error can be time-consuming. That's why the concept of momentum in backpropagation is used to speed up this process. It states that previous weight changes must influence the present direction of movement in weight space. Simply put, an aggregate of past weight changes is used to influence a current one.
During optimization, gradients can change direction, complicating the overall process. This momentum technique ensures optimization continues moving in the right direction and improves the neural network's performance.
What is a backpropagation algorithm pseudocode?
The backpropagation algorithm pseudocode is a basic blueprint that developers and researchers can use to conduct the backpropagation process. It's a high-level overview with plain language, human-readable instructions and code snippets to perform the most essential tasks in the process. Any common programming language can be used to write it, such as Python and other object-oriented programming languages
While this overview covers the essentials, the actual implementation can be far more complex. The pseudocode covers the steps that need to get done; it typically reads like a series of actions, and within it are all the core components and calculations that the backpropagation process will involve. This includes the computing of gradients and updating of weights, for example. Each pseudocode instance is pertinent to a specific context.
What is the Levenberg-Marquardt backpropagation algorithm?
The Levenberg-Marquardt algorithm is another technique that helps adjust neural network weights and biases during training. However, within the context of training neural networks, it isn't an alternative or replacement for a backpropagation algorithm, but rather an optimization technique used within backpropagation-based training.
To reduce neural network errors, Levenberg-Marquardt blends gradient information from the gradient descent method with insights from what's called the Gauss-Newton algorithm. Here, gradient information is represented in a curved format using mathematical matrices as a method of guiding updates and speeding up what would take a traditional gradient descent method longer to complete.
History of backpropagation
Backpropagation was invented by Paul Werbos in 1974 as a general optimization method extending to the idea of propagation errors in multilayer networks. However, it went unrecognized at the time. It wasn't until 1986, when David Rumelhart, Geoffrey Hinton and Ronald Williams published a paper titled "Learning Representations by Back-Propagating Errors," that backpropagation began gaining more attention. The paper showed the effectiveness of the algorithm for training multilayer networks and helped renew the popularity of neural networks.
It isn't easy to understand exactly how changing weights and biases affects the overall behavior of an ANN. That was one factor that held back more comprehensive use of neural network applications until the early 2000s, when computers provided the necessary insight. The development of deep learning in the 2000s also led to another resurgence of backpropagation, as it became a critical method for training deep neural networks.
Today, backpropagation algorithms have practical applications in many areas of AI, including OCR, natural language processing and image processing.
Many other ML algorithms are also considered to be supervised machine learning. Learn more about different types of machine learning, including unsupervised, semisupervised and reinforcement learning.